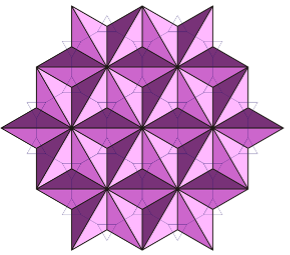
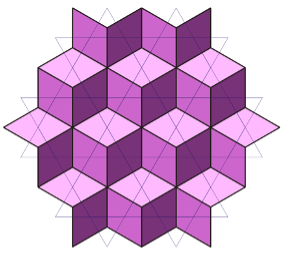
A TESSELLATION is the periodic repetition of the same figure covering a plane without overlapping or holes. The figures used to cover the surface, tessellations, are often polygons, regular or not, but they can also have curved sides or be without any vertices. Below are some “regular” tessellations in that they each use only one geometric shape:
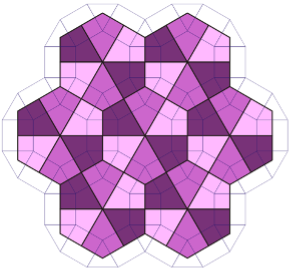

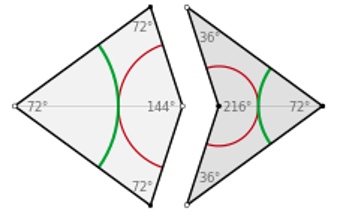
In 1974 Roger Penrose and Robert Ammann discovered various irregular tessellations, that is, making use of multiple geometric figures in a single tessellation, including the kite and the dart:

How to play
It is the periodic repetition of the same figure covering the floor without overlapping or holes. Your floor could be an example of this. It is easy to tessellate a floor with rectangular, hexagonal tiles or triangular by replicating the same figure in different positions. But what if you have edges, can you tessellate? Choose shapes and combine them to cover the whole plane, you will find that there are different ways to tessellate, but traceable to two types of tessellation:
A tessellation is PERIODIC if it involves regular repetition of the tessellation, which in such cases is always a polygon. A polygon, regular or irregular, tessellates if its interior angle is submultiple of an angle of 360°. Which polygons tessellate? Does a regular pentagon tessellate the plane?
A tessellation is NON PERIODIC if it is impossible to detect a pattern that repeats itself identically indefinitely, even if at first glance it appears to be there. Among the most famous tessellations that generate nonperiodic tessellations are those of the mathematician Penrose, the arrow and the kite, made from a rhombus with angles of 72° and 108°.
Teaching links: GEOMETRY – Covering the plane or space with repeating regular figures is a classic problem in geometry, even before it was an artistic one. It involves a whole range of geometric concepts such as reflections, rotations, translations and, not least, the golden section. More generally, objects such as the tangram/stomachion, the magic square, the Tower of Hanoi, and the tessellated plane put systems with very precise rules into game form, allowing a whole series of results that are often invisible at the outset to be deduced and thus predicted with certainty. Although this does not make them trivial or easy to solve (the case of Stomachion is emblematic). Quite the opposite of games based on chance, such as games of chance.
Teaching links: PHILOSOPHY – What Aristotle began more than 2,000 years ago, a team of 30 undergraduate students at the Massachusetts Institute of Technology is continuing now. They are starting with a recent mathematical result that has breathed new life into the age-old hunt for geometric shapes that can tessellate, that is, perfectly fill, three-dimensional space. “It is exciting to know that some of the greatest minds of all time have been working on this topic.
Playing floor tessellation can be a very rewarding experience, for young and old alike. Often a time for parents and children to have fun together, the advice is to foster these moments, starting with the simple tessellation exercise, you can then ask them to explore more original, artistic solutions, and only at the end, only when the experience has been enjoyed, will it be possible to also tell about the mathematics behind it.
Some figures, e.g. triangle, square, rectangle, hexagon, etc., allow us to make a complete tessellation, while others do not. How come? And how can the result be predicted? Mathematics helps us: in general, it is enough to add up the amplitudes of the angles formed at any of the meeting points of the tessellations to figure it out. If the result of adding the amplitudes of these angles is other than 360°, it will not be possible to make a complete tessellation, otherwise yes. If we then impose for the whole tessellation the use of only one regular polygon, that is, with equal sides and angles, we have only 3 possible configurations. In fact, in this case the measure of the angles of the tessellation will have to be an integer divisor of 360°and therefore only the equilateral triangle (60°), the square (90°) and the regular hexagon (120°) will do.
In nature there are infinite tessellations, that is, whose basic geometric shape is continuously repeated. An example is the hexagon in the bee hive:

Dutch artist Maurits Cornelis Escher is famous for his tessellations that often depict animals such as fish, birds, and horses.

How to build
EXHIBIT MATERIAL:
- no. 2 base pallet 120×180 cm
- Moulds for tessellation (in MDF)
according to drawing, as desired in
colors, but in the shapes indicated (10 cm side): kites, darts, equilateral triangles, regular pentagons, right triangles, scalene triangles.
- Red MDF frame
- no. 2 honeycomb cardboard
shelves (100x140cm)x2 - no. 4 cardboard panels (40x15cm)
with descriptions of different types
of dowel






