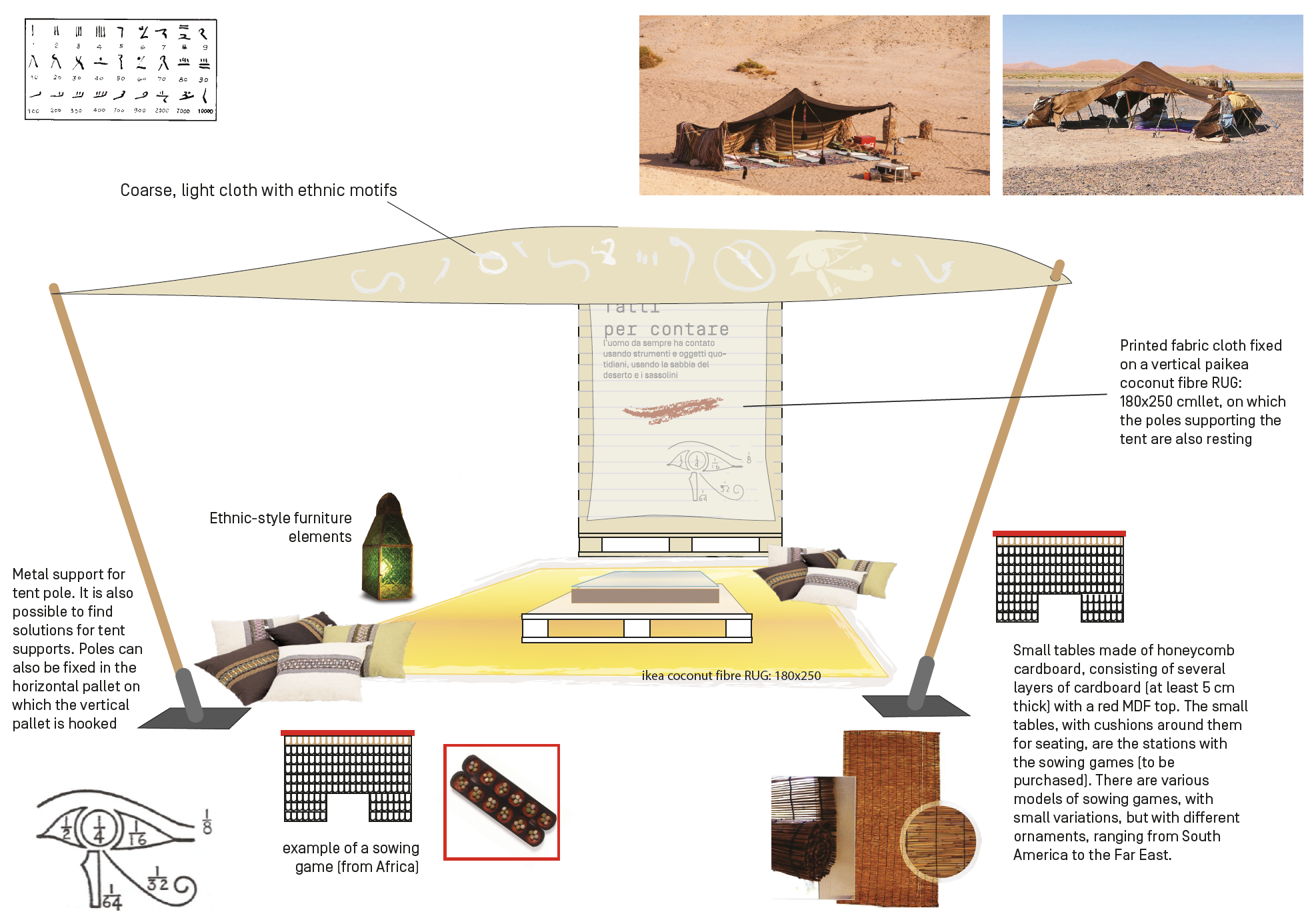
This is the first exhibit of the tour. One enters under a Bedouin tent, under which there is a shrine with reproductions of various ‘mathematical’ objects representing some of the oldest objects used for counting, a bone with notches on it, a system of strings with knots (quipu) and some terracotta cones, placed inside a shrine with sand.







How to play
The animator, using pebbles (‘calculus’ in Latin) asks how one can count without having numbers, and proposes measuring or counting using only pebbles or strings. Stories can also be told under the tent (see attached documents) of how people began to count, using reproductions of the oldest objects used to do so.
MANCALA (SEEDING GAMES)
The seeding games are a family of board games widespread in much of the world (especially in Africa, the Middle East, South-East Asia and Central America).
The similarity of many aspects of the game with agricultural activity and the simplicity of the board and pieces, the large number of variants and their spread throughout the world suggest an extremely ancient origin; according to some, perhaps close to the very origins of civilisation.

These are ancient games that were the precursors of backgamon. The game is a universal tool that helps people learn more about themselves and others. Play is pastime, recreation and at the same time a vehicle that allows one, almost without realising it, to acquire skills useful in the development of each individual.
Mancala is an ancient African game that belongs to the family of sowing games. In one of the most popular versions, mancala is a board that has two parallel rows of six holes, one row for each player. In each hole four tokens, the seeds, are placed. On the sides two receptacles, the mancalas, contain the earned seeds. They can be beans, seeds, berries or grains, stones or as we did, shells.The board represents heaven and earth and in some cultures the movement of the pawns simulates the acts of sowing and harvesting.
RULES
In turn, each player takes all the tokens contained in one of the six holes in his row and, proceeding anti-clockwise, ‘sows’ them in the holes that lie in succession after the one from which he took them, one per hole including of course his own mancala.
If, during play, either player arrives with his last token in an empty hole or one containing more than two marbles, he takes none. If, on the other hand, the hole contains 1 or 2 checkers, excluding the one he has laid down, he is entitled to take all the checkers in the hole, including his own.
The game ends when either player no longer has enough checkers to move. In this case the opponent captures the remaining checkers and the player who has captured the most checkers wins. However, to prevent such a situation from arising too early in the game, it is forbidden to completely empty the opponent’s ranks, thus preventing him from making a counter-move, unless all possible moves block the opponent in any case. A player who does not respect this last rule is punished: his opponent captures all the pawns left in the game.
ISHANGO BONE
The earliest evidence of human use of numbers dates back more than 35,000 years and consists of bones carved with notches that are thought to indicate some kind of counting-days, animals? The most famous ancient find is the bone from Ishango, a village located in the Democratic Republic of Congo, dated between 20,000 B.C. and 18,000 B.C. and dating to the Upper Paleolithic.
Why? The organization of the notches into three asymmetrical pairs implies that this arrangement was intentional. What can be inferred is a first step toward the construction of a true number system. Line A-reading from left to right-begins with 3 notches and is followed by 6 notches, twice as many. The same for the following: 4 notches, then 8, and then reversing the system with 10 being followed by 5. These numbers, then, suggest an understanding of multiplication and division by 2. In addition, numbers of notches on either side of rows B and C seem to indicate a more important calculating skill. The numbers are all odd: 9, 11, 13, 17, 19, and 21. Those notched in row B are all prime numbers between 10 and 20, while those on row C are made up following the rule 10 + 1, 10 – 1, 20 + 1, and 20 – 1.
Row A 
Row B 
Row C 
Fun fact: The Ishango bone is the fibula of a baboon with a sharp quartz scale grafted to one end, probably used for carving. Among the hypotheses that best explain the arrangement of these notches, scholars assess it to be the computation of a day sequence and specifically a lunar month. The bone was discovered in 1960 by Jean de Heinzelin de Braucourt (Belgium) during an exploration of the former Belgian Congo. It was found near Ishango, on the Uganda-Congo border. The people who lived there in 20,000 B.C. may have been among the first to use a numerical system. The find is on display at the Royal Museum of Natural Sciences in Brussels.
QUIPU
In the Quechua language (an indigenous language native to South America)the quipo or quipu is a set of ropes knotted at regular intervals and tied to a larger, shorter rope that holds them up.
Why? Some civilizations that developed in Latin America, which had not yet invented numbers, had to engineer themselves to solve mathematical problems concerning census, taxes, counting items bought or sold, astronomical calculations, description of historical and economic events, and of course arithmetic operations. It is possible that the quipu was used by Inca administrators to perform addition, subtraction, multiplication and division for the inhabitants. Some nodes recorded on the quipu were not numbers, but “labels” of numbers that were used as a code, just as we use numbers to indicate objects, places, people, etc. Other elements of the quipu, such as the position and distance between strings, and the colors used, also represented information.

Fun fact: To this day, the quipu remains an object whose use has not been totally explained. Quipu were constructed to remain unaltered: after being wet and allowed to dry, they were glued together with special resins. Even today, a simpler version of the quipu is used by Peruvian and Bolivian herders. Quipus may consist of only a few strings, but some go as high as 2,000.
How to build
EXHIBIT MATERIAL:
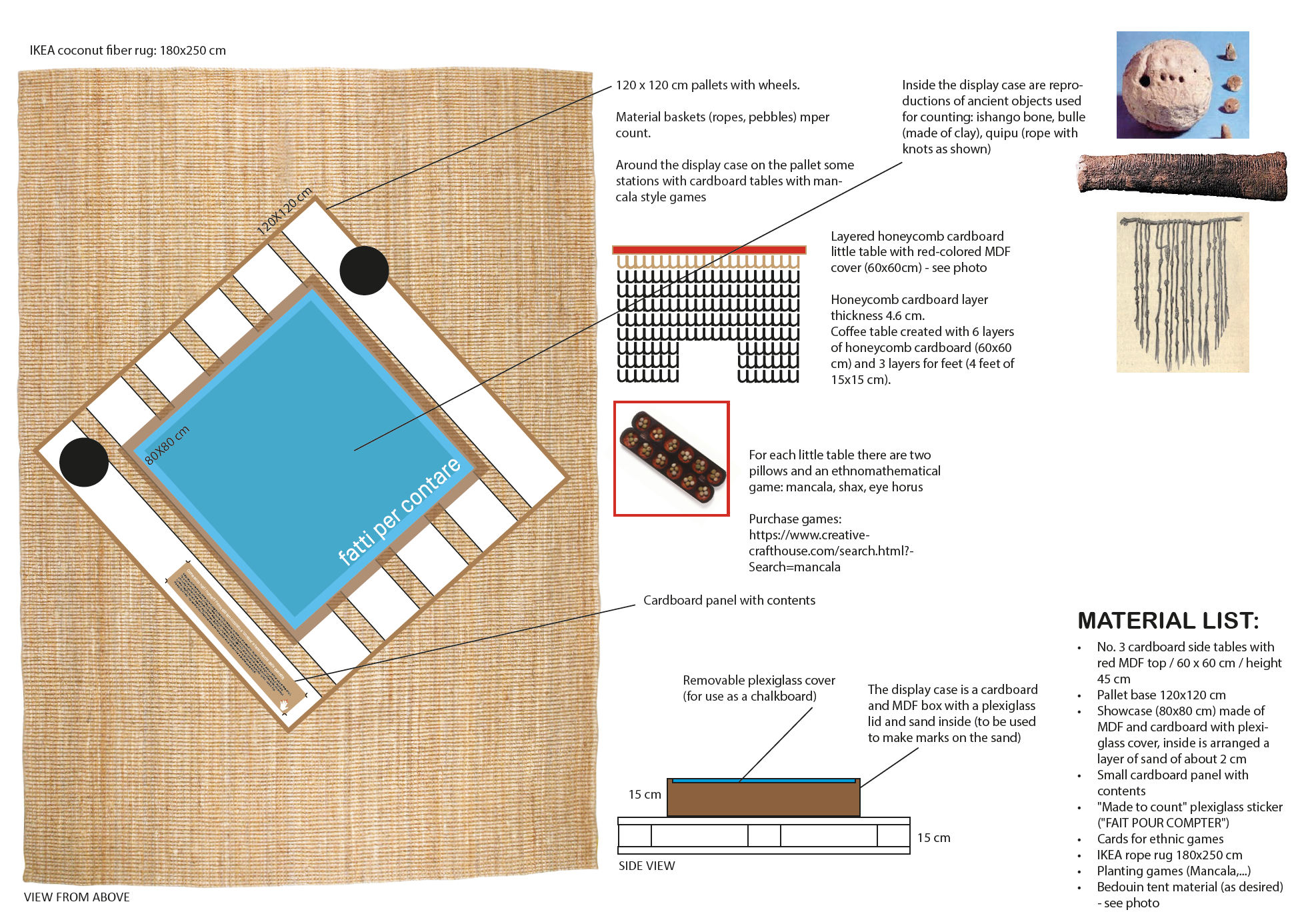
- n. 3 cardboard side tables with red MDF top / 60 x 60 cm / height 45 cm
- n. 1 pallet base 120×120 cm
- n. 1 vertical pallet 120×200 cm // to be placed on a horizontal pallet
- n. 1 horizontal pallet 120×80 cm
- Showcase (80×80 cm) made of MDF and cardboard with plexi-glass cover // inside is arranged a layer of sand of about 2 cm Small cardboard panel with contents
- “Made to count” plexiglass sticker (“FAIT POUR COMPTER”)
- Cards for ethnic games and pebbles with storage baskets
- IKEA rope rug 180×250 cm
- SEEDING games (Mancala)
- Bedouin tent material (as desired) // see photo // To be arranged according to the spaces and needs of the person setting up
- Reproduction of femur bone with incisions
- Clay spheres with hollow marks and clay cones
- Reproduction of Quipu, see photograph in dossier
CLICK AND DOWNLOAD PRINT-READY .PDF FILES:
CARDBOARD PANEL 65×10 cm (ITA)
CARDBOARD PANEL 65×10 cm (FRA)
CARDBOARD PANEL 65×10 cm (DE)
ADHESIVE THECA (ITA)
ADHESIVE THECA (FRA)
ADHESIVE THECA (DE)