How can we explain the relationship between phenomena that vary in time and space and make predictions about their evolution? One possible way is to build models that can represent reality, introducing abstractions into these models that simplify the complexity of the world around us. This is what statisticians and data scientists do. The Monte Carlo method – named after the city’s famous Casinò – is a tool used to calibrate these models using available data so that the resulting predictions are accurate.
How to play
Create an irregular figure by combining the pieces of wood joined by Velcro and place it in the center of the red square that has a side equal to 1 m and therefore an area equal to 1 m^2. How can you calculate the area of the irregular figure you created?
Here’s a possible solution: imagine that you dropped an even rain of ping-pong balls inside the red square: if you counted the balls and found that half of them fell inside your figure constructed from the sticks, what could you deduce about its area? That it is about half that of the square.
What if the balls dropped inside the constructed figure were one-third of the total? You would think that the area of the figure is about one-third of 1 m^2.
This is a method that gives an estimate of area not an exact value. If I want to increase the accuracy of my estimate, I can use smaller objects, for example, chickpeas or sand instead of ping-pong balls. Of course instead of counting chickpeas or grains of sand the can be weighed.




We understand the importance of computers: a suitably programmed computer can simulate the random fall of a large number of chickpeas, it can count the number of chickpeas that fell inside the irregular figure and those outside, so as to estimate the area of a generic figure as an appropriate fraction of that of the outer square, which, we recall, is equal to 1 m2.
So far we have reasoned with plane figures, but the reasoning can be extended to irregular solids as well. Think of a slice of cheese with holes in it, how can we calculate its volume? Or how can we compare the trunk capacity of a subcompact car with that of a station wagon? We could calculate the number of suitcases each trunk can hold (the suitcases play the role of ping-pong balls here), and if we wanted to increase the accuracy of our assessment (estimation) we could replace the suitcases with tennis balls… now don’t think about filling the trunk of your parents’ car with chickpeas or, even worse, sand, to estimate its capacity – they wouldn’t be very happy!
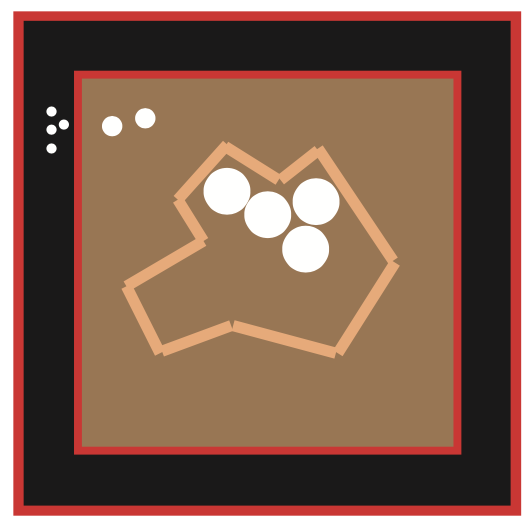
Strategy: You fill the red square (and consequently also the area bounded by the sticks) with a layer of balls. We count the balls (we weigh the chickpeas or sand if we want more precise estimates) inside that red square (including those inside the figure). We denote this value by X. We then count only the balls inside the figure bounded with the little sticks. We denote this value by Y. A simple proportion will lead to an estimate of the area.
For example, let’s imagine that we fit exactly 100 balls in the square. And let’s imagine that the little woods delimit exactly ¼ of the area inside the square. Inside the perimeter of the little woods will then fit about 25 balls. The corresponding area, denoted by A, is then obtained by solving the proportion:
25 : 100 = A : 1m2
A = 25/100 x 1 m2= 0.25 m2
The Department of Energy’s Oak Ridge National Laboratory’s Frontier supercomputer earned the top spot on May 30, 2022, as the world’s fastest in the 59th TOP500 list, with 1.1 exascale performance. The system is the first to achieve an unprecedented level of processing performance known as exascale, a threshold of one quintillion calculations per second.
A Monte Carlo simulation is a randomly evolving simulation. In this video, I explain how this can be useful, with two fun examples of Monte Carlo simulations: The first model shows how pi can be determined with Monte Carlo sampling, and in the second part of the video we will take a look how animations can be rendered with Monte Carlo path tracing.
How to build
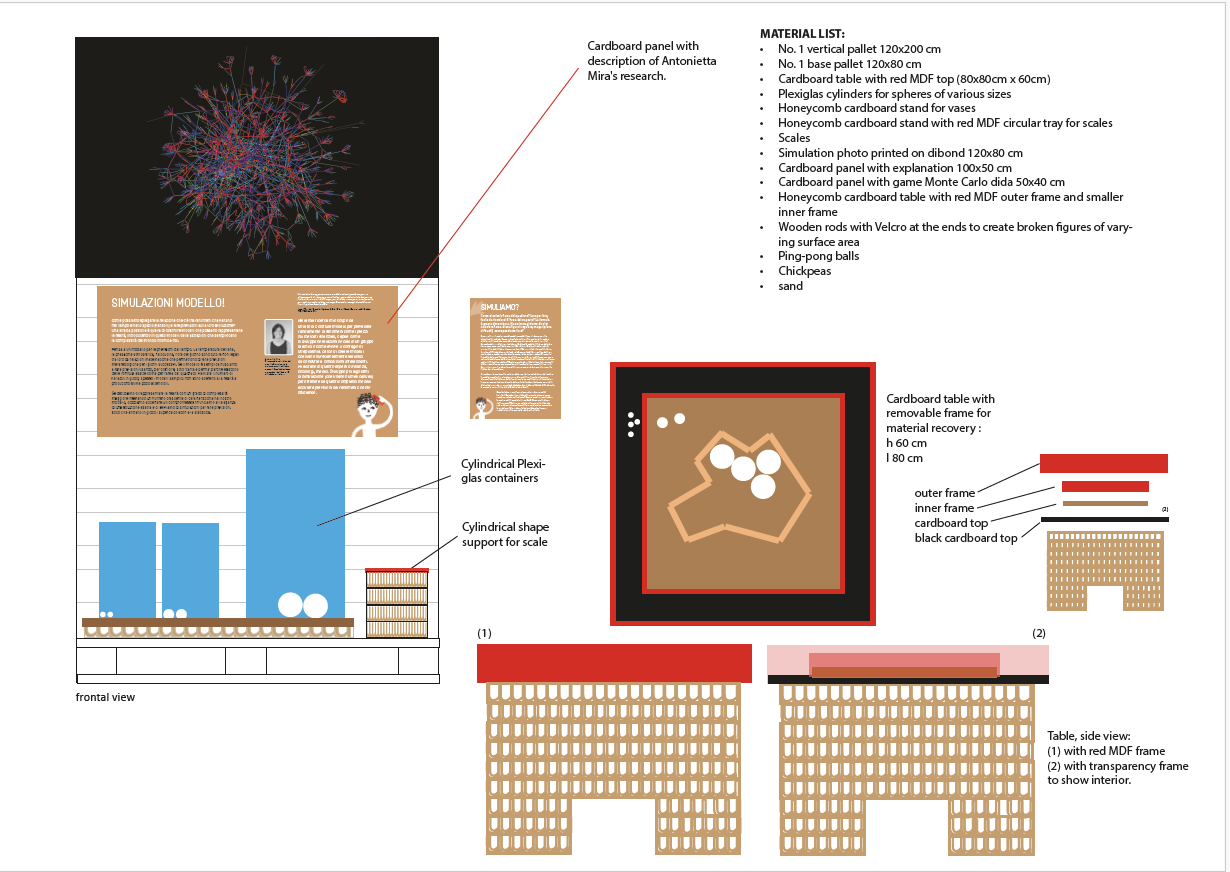
EXHIBIT MATERIAL:
- n. 1 vertical pallet 120×200 cm
- n. 1 base pallet 120×80 cm
- Cardboard table with red MDF top (80x80x60cm)
- Plexiglas cylinders (vases) for spheres of various sizes
- Honeycomb cardboard stand for vases
- Honeycomb cardboard stand with red MDF circular tray for scales
- Scales
- Simulation photo printed on dibond 120×80 cm
- Cardboard panel with explanation 100×50 cm
- Cardboard panel with game Monte Carlo dida 50×40 cm
- Honeycomb cardboard table with red MDF outer frame and smaller inner frame
- Wooden rods with velcro at the ends to create broken figures of varying
- surface area
- Ping-pong balls
- Chickpeas
- sand
CLICK AND DOWNLOAD PRINT-READY .PDF FILES:
- CARDBOARD PANEL 50X40 CM (FRA) (.PDF)
- CARDBOARD PANEL 50X40 CM (FRA) (.AI)
- CARDBOARD PANEL 100X50 CM (FRA) (.PDF)
- CARDBOARD PANEL 100X50 CM (FRA) (.AI)
- CARDBOARD PANEL 100X50 CM (ITA) (.PDF)
- CARDBOARD PANEL 100X50 CM (ITA) (.AI)
- CARDBOARD PANEL 50X40 CM (ITA) (.PDF)
- CARDBOARD PANEL 50X40 CM (ITA) (.AI)
- SIMULATION PHOTO FOR DIBOND (.TIF)